Formes

Pour faire les TCOs de base on a besoin que trois formes (dessins) : une forme droite, une forme courbe et une forme biaise :

D’autre formes viendrons par la suite, mais restons pour l’instant sur ces trois formes. Ces trois formes ne diffèrent que par leur dessin (leur PShape).

Suivant les bonnes habitudes de la programmation objet on va écrire une classe de base qui regroupe tout ce qui concerne la gestion commune des trois formes. Cette classe de base sera appelée Forme, cette classe peut être "abstraite" car elle n’est pas destinée à être instanciée. Pour gérer les particularités des trois formes dont on a besoin, on écrit trois classes qui héritent de la classe de base (Forme) et qui gèrent les parties spécifiques à chaque forme.

La classe de base

Voici un début de classe de base Forme :

abstract class Forme { 
  PShape s; // le contour de la forme

  Forme() { // constructeur
    s=createShape(); // creation de la forme
  }
  
  void dessiner(int c) { 
    s.setFill(c); // remplissage de la forme avec la couleur c
    shape(s,0,0); // dessin de la forme
  }
}

Comme on peut le voir le contour de la forme n’est pas défini (c’est pourquoi cette classe n’est pas instanciable), cela va être le rôle des classes dérivées.

Les classes dérivées

• La forme courbe

Commençons par la forme courbe (arc 45°), son contour peut être repris intégralement de l’article précedent (Processing pour nos trains) :

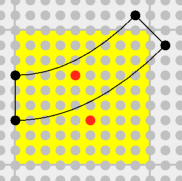
  beginShape(); // debut du contour de la forme
  vertex(0,3); // point de depart
  quadraticVertex(4,3, 8,-1); // courbe Bezier quadratique
  vertex(10,1); // ligne droite
  quadraticVertex(5,6, 0,6);  // courbe Bezier quadratique
  endShape(CLOSE); // fermeture du contour de la forme (ligne droite)

Cette description du contour était dans le setup(), elle va se retrouver naturellement dans le constructeur de notre nouvelle classe :

class FormeArc45 extends Forme { 
  FormeArc45() { // constructeur (petit arc de 45°)     
    s.beginShape();
    s.vertex(0,3); s.quadraticVertex(4,3, 8,-1); s.vertex(10,1); s.quadraticVertex(5,6, 0,6); 
    s.endShape(CLOSE);
  }
}

La classe FormeArc45 hérite de la classe de base Forme et la complète avec un contour particulier, cette nouvelle classe est parfaitement utilisable.

• La forme droite

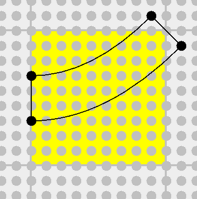
Dans l’article précédent la forme droite était réalisée avec un rectangle, comme il a été dit précédemment par soucis d’unification on va réaliser aussi cette forme avec une PShape, donc avec un contour. Le dessin suivant matérialise ce contour :

Les coordonnées des points sont : (0,3) (9,3) (9,6) (0,6).

De la même façon que pour la forme courbe, pour la forme droite on a la classe FormeDroit :

class FormeDroit extends Forme { 
  FormeDroit() { // constructeur
    s.beginShape();
    s.vertex(0,3); s.vertex(9,3); s.vertex(9,6); s.vertex(0,6);
    s.endShape(CLOSE);
  }
}

• La forme biaise

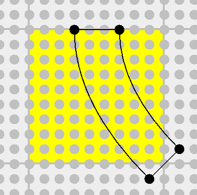
Il ne manque plus que la forme biaise, qui est nouvelle par rapport à l’article précédent. Voici son contour :

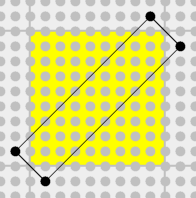
Les coordonnées des points sont : (8,-1) (10,1) (1,10) (-1,8).

Sur le modèle de la classe FormeDroit on peut écrire la classe FomeBiais, seul les points du contour changent :

class FormeBiais extends Forme { 
  FormeBiais() { // constructeur
    s.beginShape();
    s.vertex(8,-1); s.vertex(10,1); s.vertex(1,10); s.vertex(-1,8);
    s.endShape(CLOSE);
  } 
}

Transformations

Nous avons maintenant les trois formes de base, à l’usage on se rendrait vite compte que ces trois formes sont nettement insuffisantes, il en faut plein d’autres. Mais ces formes manquantes peuvent être facilement obtenues en appliquant aux formes de base des transformations. Il s’agit de ce que l’on appelle des "transformations affines", tout bon logiciel de dessin offre de telles transformations et c’est le cas avec Processing. Nous aurons besoin de plusieurs transformations :

• une translation pour pouvoir placer les formes où l’on veut sur le TCO
• une rotation de 90°
• une symétrie par rapport à un axe vertical (ou horizontal)

Processing a des fonctions intégrées pour faire des translations et des rotations, mais pas de symétrie. De plus pour les rotations il faut "bricoler" un peu pour fixer le centre de la rotation et puis les angles de rotation sont exprimées en radians. Ces considérations nous amènent à écrire nos propres transformations, bien adaptées à nos besoins. Cela se fait avec des matrices de transformations affines.

L’idée est de faire une multiplication entre les coordonnées d’un point et une matrice de transformation pour obtenir les coordonnées d’un nouveau point :

[ x']   [  m00  m01  m02  ] [ x ]   [ m00*x + m01*y + m02 ]
[ y'] = [  m10  m11  m12  ] [ y ] = [ m10*x + m11*y + m12 ]
[ 1 ]   [   0    0    1   ] [ 1 ]   [           1         ]

Les coordonnées de l’ancien point sont (x,y) celle du nouveau point sont (x’,y’), les m00, m01, …, m12 sont les coefficients de la matrice de transformation. La matrice de transformation est une matrice 3x3 dont seules les deux premières lignes sont utiles, ces six coefficients seront en fait les paramètres utiles des transformations.

Comme on veut pouvoir combiner les transformations, il faut que les matrices de transformation soient carrées (pour pouvoir faire des multiplications de matrices entre elles), la dernière ligne contient donc des éléments "neutres" vis à vis de la multiplication de matrice (0,0,1). De la même façon il faut que le vecteur contenant les coordonnées d’un point (x,y) ait trois éléments pour pouvoir le multiplier avec les matrices, un 1 est donc ajouté.

Les transformation dont on a besoin sont générales et elles s’appliquent à n’importe quelle forme. On va donc les mettre sous forme de méthodes dans la classe de base Forme.

• Translation

Commençons par la translation, cela donne une méthode comme cela :

void translation(float dx,float dy) { s.applyMatrix(1,0,dx, 0,1,dy); }

La méthode applyMatrix() de la classe PShape a comme paramètre les deux premières lignes de la matrice de transformation.

A partir des coordonnées (x,y) d’un point on obtient les nouvelles coordonnées x’=x+dx et y’=y+dy ce qui réalise bien une translation du point

Pour rendre plus aisée l’utilisation des méthodes de transformation, en fait pour pouvoir les enchaîner, on va les modifier pour qu’elles aient un résultat, complètement artificiel, qui soit une référence à la classe sur laquelle elles sont appellées (ici des formes) :

Forme translation(float dx,float dy) { s.applyMatrix(1,0,dx, 0,1,dy); return this; }

• Symétrie

Passons à la symétrie, on a choisi, arbitrairement, une transformation faisant une symétrie autour d’un axe vertical passant par le centre de la forme :

Forme symetrie() { s.applyMatrix(-1,0,9, 0,1,0); return this; }

La sous matrice ((-1,0)(0,1)) est en fait une matrice de symetrie classique autour d’un axe vertical passant par le point (0,0), le 9 est juste une translation en x (d’une case du TCO) pour avoir une symétrie par le centre de la forme.

• Rotation

Concernant la rotation, on a choisi une rotation de 90° dans le sens des aiguilles d’une montre, avec le centre de rotation au centre de la forme :

Forme rotation() { s.applyMatrix(0,-1,9, 1,0,0); return this; }

La sous matrice ((0,-1)(1,0)) est en fait une matrice de rotation classique autour du point (0,0), les éléments étant les sinus et cosinus de 90°, le 9 est juste une translation en x (d’une case du TCO) pour avoir une rotation par le centre de la forme.

Par commodité, on ajoute une méthode de rotation qui repète la rotation à 90° plusieurs fois :

Forme rotation(int n) { for (int i=0; i<n; i++) rotation(); return this; }

La compréhension de ces transformations n’est pas indispensable pour fabriquer son propre TCO, pour plus d’informations sur les transformations voir Matrices de transformation. Exemples de symétrie et de rotation :

Transformations

Original	Symetrie	Rotation

La classe Forme complète :

abstract class Forme { 
  PShape s; // le contour de la forme

  Forme() { // constructeur
    s=createShape(); // creation de la forme
  }
  
 Forme translation(float dx,float dy) { s.applyMatrix(1,0,dx, 0,1,dy); return this; }
 Forme symetrie() { s.applyMatrix(-1,0,9, 0,1,0); return this; }
 Forme rotation() { s.applyMatrix(0,-1,9, 1,0,0); return this; }
 Forme rotation(int n) { for (int i=0; i<n; i++) rotation(); return this; }

  void dessiner(int c) { 
    s.setFill(c); // remplissage de la forme avec la couleur c
    shape(s,0,0); // dessin de la forme
  }
}

D’autres choix de transformations sont aussi possibles pour obtenir toutes les formes dont on a besoin.

Pavés

Avec les formes on va faire des pavés, quelques exemples :

Toujours en suivant les bonnes habitudes de la programmation objet on va écrire une classe de base qui regroupe tout ce qui concerne la gestion commune des pavés. Cette classe de base sera appelée Pave, cette classe peut être "abstraite" car elle n’est pas destinée à être instanciée. Pour gérer les particularités des Pavés, on écrit des classes qui héritent de la classe de base (Pave) et qui gèrent les parties spécifiques à chaque pavé.

Un pavé est composé d’une ou plusieurs formes qui vont êtres dessinées (les unes sur les autres) pour réaliser le dessin dont on a besoin pour schématiser une portion de voie ou un appareil de voie. Le pavé a donc une variable de type tableau pour mémoriser ces formes, mais aussi une méthode pour dessiner ces formes.

La classe de base

Voici un début de classe Pave :

abstract class Pave {
  Forme[] formes; // les formes
  int couleur=GRIS; // couleur pour le pave
  
  Pave(Forme... fs) { formes=fs; } // constructeur

  void dessiner() { int l; 
    l=formes.length; // le nombre de formes
    for (int i=0; i<l; i++) { // pour toutes les formes
      if (i==l-1) formes[i].dessiner(couleur); // la derniere forme (gris ou autre)
      else        formes[i].dessiner(GRIS_FONCE); // les autres formes (gris fonce)
    }
  }

  void colorer(int c) { couleur=c; }
}

Le constructeur du pavé est un peu particulier, il peut être appelé avec un nombre quelconque de paramètres (du même type), notation avec les trois points, ces paramètres seront vus en fait comme un tableau.

La méthode dessiner() dessine toutes les formes en gris foncé, sauf la dernière qui est dessinée en gris par défaut, couleur qui peut être changée avec la méthode colorer().

Les classes dérivées

On peut maintenant écrire des classes pour les pavés dont on a besoin pour les TCOs. Ces classes héritent de la classe de base Pave, il faut juste qu’elles précisent les formes utilisées pour dessiner le pavé. Cela se fait dans le constructeur en fournissant au constructeur de la classe de base une liste de formes, notation super(forme1,forme2,forme3,…).

Le pavé droit :

class PaveDroit extends Pave {
  PaveDroit() { super(new FormeDroit()); } // constructeur
}

Le pavé biais :

class PaveBiais extends Pave {
  PaveBiais() { super(new FormeBiais()); } // constructeur
}

Le pavé arc 45° :

class PaveArc45 extends Pave {
  PaveArc45() { super(new FormeArc45()); } // constructeur
}

Il faut maintenant passer aux appareils de voie, ceux-ci sont constitués de plusieurs formes, commençons par une aiguille droite :

class PaveAiguilleDroite extends Pave {
  PaveAiguilleDroite() { super(new FormeArc45(),new FormeDroit()); } // constructeur
}

Le pavé comporte deux formes, une droite et une courbe (arc45). Suivant l’ordre dans lequel sont dessinées les deux formes, l’aiguille est droite ou déviée.

Passons à l’aiguille biaise, ah ! il y a un problème, on n’a pas la forme arc convenable. Qu’a cela ne tienne on va faire tourner la forme arc existante pour avoir la forme dont on a besoin, d’une rotation de 180° ce qui donne deux rotations de 90° (c’est ici que la forme particulière des méthodes de transformation a toute son utilité, on pourrait enchaîner plusieurs transformations) :

class PaveAiguilleBiaise extends Pave {
  PaveAiguilleBiaise()  { super(new FormeArc45().rotation(2),new FormeBiais()); }
}

Un peu plus compliqué un pavé TJD (Traversée Jonction Double) :

class PaveTJD extends Pave { 
  PaveTJD() { super(new FormeBiais(),new FormeArc45().rotation(2),new FormeArc45(),new FormeDroit()); } 
}

On retrouve trois formes de base (droit, biais et arc45) et une forme transformée (arc45).

C’est comme du Meccano cela s’écrit pratiquement tout seul. On trouvera dans les fichiers accompagnant l’article tous les autres appareils de voie construits sur le même principe (aiguille symétrique, TJS et aiguille triple, ...).

Transformations

Comme pour les formes, on n’a pas encore à disposition tous les pavés dont on aura besoin pour les TCOs (surtout pour les appareils de voie), il faut donc recourir aux transformations (rotations et symétrie), on aura aussi besoin d’une translation pour placer les pavés sur le TCO.

On va donc rajouter à la classe de base des transformations (ce sont les mêmes que pour les formes) :

  Pave rotation() { for (Forme f : formes) f.rotation(); return this; }
  Pave symetrie() { for (Forme f : formes) f.symetrie(); return this; }
  Pave rotation(int n) { for (int i=0; i<n; i++) rotation(); return this; }
  Pave translation(float x,float y) { for (Forme f : formes) f.translation(x,y); return this; }

Ces méthodes ne font qu’appeler la même transformation sur toutes les formes. Les "for" sont un peu particuliers, ce sont des "forall", il faut les "lire" de la façon suivante : pour toutes les formes nommées "f" de la listes de formes "formes" on fait les instructions qui suivent.

Comme pour les formes ces méthodes retournent un résultat "artificiel" pour pouvoir les enchaîner facilement.

Manoeuvre

Il faut pouvoir manoeuvrer les appareils de voie, le TCO doit pouvoir refléter la position réelle des appareils de voie du réseau. On va pour cela utiliser une méthode spécifique manoeuvrer().

La manoeuvre des appareils de voie va se faire en permutant les formes du pavé (d’autres façons de faire sont possibles). Un problème vient du fait que certains appareils de voie sont constitués en fait de deux aiguilles imbriquées (TJD, TJS et triple) et il faut pouvoir préciser quelle aiguille on veut manoeuvrer, un booleen va alors servir pour préciser laquelle. Par commodité une méthode sans paramètre est ajoutée pour les aiguilles simples.

La mise en oeuvre de cette méthode va respecter les usages de la programmation objet, à savoir dans la classe de base on met une méthode qui traite du cas général, ce cas général ici consiste à ne rien faire (méthode vide). On ne manoeuvre que les appareils de voie et éventuellement les signaux, la méthode sera redéfinie dans les classes dérivées qui en ont besoin.

Cette façon de faire permet d’avoir dans la classe de base toutes les méthodes concernant toutes les variétés de pavés constituant ainsi une interface entre les autres objets qui utilisent les pavés et les pavés eux mêmes. On peut ainsi appeler des méthodes sur tous les pavés sans se préoccuper du type réel du pavé, pas besoin de tests préalables. Cette façon de faire est typique de la programmation objet.

En pratique on ajoute à la classe de base Pave les méthodes :

  Pave manoeuvrer() { manoeuvrer(false); return this; } // manoeuvre des aiguilles simples
  Pave manoeuvrer(boolean b) { return this; } // manoeuvre des aiguilles doubles (TJD TJS triple)

Il faut maintenant redéfinir la méthode manoeuvrer() dans les classes aiguille, faisons le pour l’aiguille droite. Pour manoeuvrer l’aiguille il suffit de permuter la dernière forme avec l’avant dernière (il n’y a que deux formes) :

Pave manoeuvrer(boolean b) { Forme f; f=formes[0]; formes[0]=formes[1]; formes[1]=f; return this; } // permutation

Pour les aiguilles doubles (TJD,TJS et triple) les permutations sont plus subtiles car elles dépendent du booléen, mais le principe reste le même. Voir dans les fichiers.

TCO

Il ne reste plus qu’a écrire une classe TCO. Il faut juste un tableau à deux dimensions pour mémoriser tous les pavés à afficher, une méthode de dessin et une méthode pour le construire, la construction pourrait être dans le constructeur, mais le fait de le faire dans une méthode permet de bien isoler la construction. Voici le squelette de la classe TCO :

class TCO {
  Pave[][] paves=new Pave[COLONNES][LIGNES];
  
  TCO() { construire(); } // constructeur
  
  void dessiner() { … }
  
  void construire() {  … }
}

Les deux constantes COLONNES et LIGNES donnent la taille du tableau. Le constructeur appelle juste la méthode construire() comme décrit ci dessus.

Pour les deux méthodes dessiner() et construire() cela va être un peu plus compliqué.

Méthode dessiner

La méthode dessiner() comporte plusieurs parties :

• une prise en compte de bordures (pour faire joli) avec une translation globale de tout ce qui suit
• un affichage (éventuel) de la grille sous les pavés par des dessins de carrés dans toutes les case du tableau
• un zoom global pour tout ce qui suit (sinon les pavés font 10x10 pixels)
• le dessin de tous les pavés (un à un), pour les placer dans le dessin du TCO une translation est faite pour chaque pavé en fonction de ses indices dans le tableau. Pour éviter que les translations ne s’accumulent on sauvegarde la transformation globale (translation+zoom) avant de faire la translation du pavé, puis on dessine le pavé et finalement on restaure la transformation globale pour le pavé suivant. Ces sauvegardes/restaurations sont faite par les méthodes pushMatrix() et popMatrix() de Processing qui utilisent une pile.

  void dessiner() { int l,c; Pave p;
    translate(BORDURE,BORDURE); // decalage pour la bordure
    for (l=0; l<LIGNES; l++) for (c=0; c<COLONNES; c++) { // dessin de la grille
      stroke(NOIR); noFill(); // bordure noire 1 pixel, pas de remplissage
      rect(c*TAILLE_CASE*ZOOM,l*TAILLE_CASE*ZOOM,TAILLE_CASE*ZOOM,TAILLE_CASE*ZOOM); // dessin d'un carre
    }
    noStroke(); // pas de bordure
    scale(ZOOM,ZOOM); // zoom des paves
    for (l=0; l<LIGNES; l++) for (c=0; c<COLONNES; c++) { // dessin des paves
      p=paves[c][l]; // un des paves
      if (p!=null) {
        pushMatrix(); // sauvegarde des transformations
        translate(c*TAILLE_CASE,l*TAILLE_CASE); // placement du pave dans la bonne case
        p.dessinerPave(); // dessin du pave
        popMatrix(); // restauration des transformations
      }
    }
  }

Les trois constantes TAILLE_CASE, BORDURE, ZOOM donnent respectivement la taille d’une case de la grille (9), la taille de la bordure en pixels (10) et le taux de zoom (5).

Méthode construire

Avec la méthode construire() celui qui veut dessiner un TCO n’a qu’à placer des instances de pavés où il le désire en leur faisant subir les transformations voulues. Par exemple si on veut un TCO pour des jonctions d’IPCS (Installations Permanentes de Contresens) du genre :

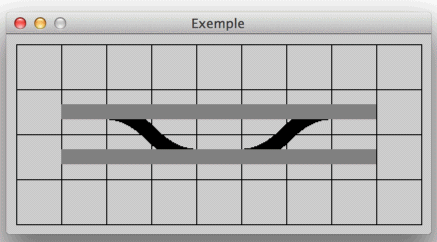
Il suffit d’écrire :

  void construire() { int l=1,c=1;
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveAiguilleDroite().symetrie().rotation(2);
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveAiguilleDroite().rotation(2);
    paves[c++][l]=new PaveDroit();
    l++; c=1; // passage à la ligne
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveAiguilleDroite().symetrie();
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveAiguilleDroite();
    paves[c++][l]=new PaveDroit();
    paves[c++][l]=new PaveDroit();
  }

Bon, pour un grand TCO c’est assez fastidieux mais on y arrive, d’autant plus que c’est très visuel. Pour faciliter la construction on peut avoir recours à des méthodes pour placer les pavés les uns après les autres automatiquement, pour avoir des intervalles vides entre pavés, pour passer à la ligne suivante, ... .

Un logiciel de dessin de TCOs est aussi en cours d’écriture.

Variante

Plutôt que d’utiliser un tableau à deux dimensions pour mémoriser les pavés, on peut utiliser une liste de pavés (ArrayList), mais dans ce cas les pavés doivent êtres "auto référencés", c’est à dire qu’ils doivent contenir en plus leur coordonnées (ligne, colonne).

Fichiers

Quelques précisions sur les fichiers accompagnant l’article.

Le dossier "Exemple_1_0" contient le programme Processing conforme aux descriptions de l’article. Le fichier "Exemple_1_0" contient des constantes, des variables et les fonctions setup() et draw(), la fonction setting() permet de définir la taille de la fenêtre avec des variables. les trois autres fichiers contiennent les formes,les paves et le TCO.

Les autres pavés de la palette on étés rajoutés, à savoir :

• un pavé aiguille biaise
• un pavé aiguille symétrique
• un pavé TJS, pour lequel une forme vide a été rajoutée
• un pavé aiguille triple
• les trois pavés croisement, pour lesquels la méthode dessiner() a été redéfinie (pour colorer les deux formes)

Améliorations

Le dossier "Exemple_1_1" contient une version améliorée du précédent. Cette "amélioration" se fait vis à vis des usages de la programmation objet, ainsi que des simplifications et ajouts.

On peut remarquer que certaines méthodes se retrouvent, avec la même écriture, dans plusieurs classes, c’est le cas des méthodes :

• manoeuvrer() dans les classes aiguilles (simples et doubles)
• dessiner() dans les classes croisement

Dans ces cas, pour ne pas avoir à répéter la méthode on ajoute une nouvelle classe (généralement abstraite) contenant la méthode. Par exemple la classe PaveAiguilleDroite() qui était écrite :

class PaveAiguilleDroite extends Pave {
  PaveAiguilleDroite() { super(new FormeArc45(),new FormeDroit()); } // constructeur
  
  Pave manoeuvrer(boolean b) { Forme f; f=formes[0]; formes[0]=formes[1]; formes[1]=f; return this; } // permutation
}

se réécrit :

class PaveAiguilleSimple extends Pave {
  PaveAiguilleSimple(Forme... fs) { super(fs); } // constructeur

  Pave manoeuvrer(boolean b) { Forme f; f=formes[0]; formes[0]=formes[1]; formes[1]=f; return this; } // permutation
}

class PaveAiguilleDroite extends PaveAiguilleSimple {
  PaveAiguilleDroite() { super(new FormeArc45(),new FormeDroit()); } // constructeur
}

De même pour les classes PaveAiguilleBiaise et PaveAiguilleSymetrique qui héritent aussi de la classe PaveAiguilleSimple. On a rajouté un étage dans l’héritage, mais on a supprimé une méthode redondante. Cette façon de faire est aussi typique de la programmation objet.

La même transformation est faite pour les classes aiguille double (TJD, TJS et aiguille Triple) qui héritent de la classe PaveAiguilleDouble, ainsi que pour les classes croisement qui héritent de la classe PaveCroisement, pour ne pas répéter la méthode dessiner().

Une méthode vertex() a été rajoutée à la classe Pave. Cette méthode prend en paramètres un nombre quelconque (mais pair) d’entiers représentant des coordonnées de points. Elle permet de simplifier les constructeurs des formes ne comportant pas de courbes de Béziers.

On peut aussi manoeuver les aiguilles en cliquant dans le pavé. Pour les aiguilles doubles il faut utiliser le clic gauche et/ou le clic droit (l’aiguille triple est ici un modèle asymétrique du genre Peco code 75, mais d’autres modèles sont possibles).

Aide

Une petite application Processing (dossier "Aide1") est ajoutée aux fichiers joints, elle permet de visualiser l’effet des transformations (symétrie et rotation) ainsi que la position des aiguilles. Mode d’emploi :

• le clic gauche fait une rotation du pavé
• le clic droit une symétrie du pavé
• le clic gauche, avec la touche "alt" appuyée, fait la manoeuvre d’une des aiguilles du pavé
• le clic droit, avec la touche"alt" appuyée, fait une manoeuvre de l’autre aiguille du pavé

Le code produisant le pavé est aussi affiché, il est automatiquement mis dans le presse-papier, on peut le coller directement dans l’IDE Processing dans la méthode construire() du TCO. Cette application peut être exécutée en même temps que celle fabriquant le TCO.

Toujours à titre d’aide, voici toutes les formes que l’on peut obtenir avec les transformations :

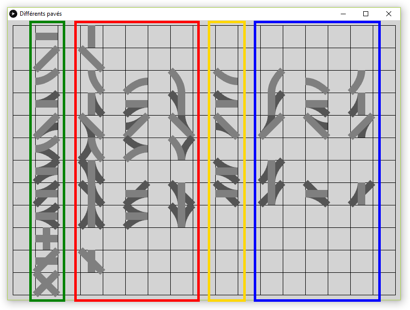
On a :

• encadré en vert, les formes de base
• encadré en rouge, les formes obtenues par rotation
• encadré en jaune, les formes obtenues par symétrie
• encadré en bleu, les formes obtenues par symétrie et rotation

Bilan

Dans cet article on a vu comment dessiner un TCO simple assez facilement. Pour un TCO réel il manque encore pas mal de choses :

• d’autres pavés : butoirs, croisements, grandes courbes, indications de sens, …
• une représentation des séparations de zones
• des signaux
• des informations textuelles
• une interface avec des gestionnaires de réseau
• la coloration des zones (pour occupation et itinéraires)
• des itinéraires
• la circulation de trains virtuels
• des manettes pour commander les trains
• …

Dans de prochains articles on verra que cela peut s’ajouter assez facilement au TCO de base décrit ici.