Dans l’article précédent (TCOs en Processing (1)) nous avons fabriqué pratiquement tous les pavés nécessaires pour faire des dessins de réseaux. Pour réaliser des TCOs il manque encore des éléments : des pavés signaux et des séparations de zones, mais aussi des améliorations des TCOs : butoir, sens, grandes courbes, quais, textes, ... . Nous allons voir comment réaliser tout cela dans cet article.
TCOs en Processing
TCOs en Processing (2)
.
Par :
DIFFICULTÉ :★★★
Pavés divers
Commençons par quelques pavés utiles, des butoirs et des sens de circulation :

Ces pavés vont nécessiter des formes qui ne seront utilisées que par un pavé, de plus ces formes sont polygonales. Pour éviter d’avoir à créer une classe spécifique pour chaque nouvelle forme, on va écrire une classe FormeSimple pour les formes simples polygonales quelconques :
class FormeSimple extends Forme {
FormeSimple(float... xys) { // constructeur
vertex(xys);
}
}Le constructeur accepte directement la liste des points du contour.
Pavés sens
Comme exemple d’utilisation de cette nouvelle classe, voici des pavés "sens", un pavé mono-sens et un pavé bi-sens :
class PaveSens extends Pave {
PaveSens() { // constructeur
super(new FormeSimple(0,3, 3.5,3, 3.5,1.5, 5.5,3, 9,3, 9,6, 5.5,6, 3.5,7.5, 3.5,6, 0,6));
}
}
class PaveBiSens extends Pave {
PaveBiSens() { // constructeur
super(new FormeSimple(0,3, 1,3, 3,1.5, 3,3, 6,3, 6,1.5, 8,3, 9,3, 9,6, 8,6, 6,7.5, 6,6, 3,6, 3,7.5, 1,6, 0,6));
}
}Les contours sont un peu compliqués mais il y a beaucoup de points sur ces contours.
Pavés butoirs
Pour les pavés butoirs il faut deux formes, une première forme qui matérialise la traverse du butoir (dessinée en gris-foncé) et une deuxième forme pour la voie (dessinée en gris). Cela donne :
class PaveButoirDroit extends Pave {
PaveButoirDroit() { // constructeur
super(new FormeSimple(9,2, 7,2, 7,7, 9,7),
new FormeSimple(7,3, 0,3, 0,6, 7,6));
}
}
class PaveButoirBiais extends Pave {
PaveButoirBiais() { // constructeur
super(new FormeSimple(4,1, 5.75,-0.75, 9.75,3.25, 8,5),
new FormeSimple(-1,8, 5,2, 7,4, 1,10));
}
}Pavés extensibles
Arc de cercle
Pour faire de jolis TCO des grand arcs de cercles sont bien utiles, on se limitera à des arcs quart de cercle de rayon quelconque, exemples :

Il faut une nouvelle forme (on ne peut pas utiliser la nouvelle classe FormeSimple ici la forme n’étant pas polygonale) :
class FormeArc90 extends Forme {
float nm=0.551784F; // nombre magique
FormeArc90(int n) { // constructeur (grand arc de 90° de rayon n)
s.beginShape();
s.vertex(0,3);
s.bezierVertex((9*(n-1)+6)*nm, 3, 9*(n-1)+6, (9*n)-(9*(n-1)+6)*nm, 9*(n-1)+6, 9*(n-1)+9); // cubique
s.vertex(9*(n-1)+3,9*(n-1)+9);
s.bezierVertex(9*(n-1)+3, (9*n)-(9*(n-1)+3)*nm, (9*(n-1)+3)*nm, 6, 0, 6); // cubique
s.endShape();
}
}Pour avoir de arcs de cercle quasiment parfaits, il faut avoir recours aux courbes de Bézier cubiques ( qui est un cas particulier des courbes de Bézier, ou B-Spline). Les courbes de Bézier cubiques ont deux points de contrôles, en choisissant judicieusement ces deux points de contrôles on obtient des arcs de cercle parfaits, le calcul de la position de ces points fait appel à un « nombre magique » (0.551784).
Il ne reste plus qu’à écrire une classe pavé :
class PaveArc90Grand extends Pave {
PaveArc90Grand(int n) { // constructeur
super(new FormeArc90(n));
taille=n;
}
}Le rayon du cercle est mémorisé dans la classe Pave dans une variable taille dont la valeur par défaut est un. Cette variable servira par la suite à faciliter le placement des pavés dans la grille du TCO.
Droit
Bien que cela ne soit pas indispensable, de longs pavés droits sont assez pratiques, la forme étant polygonale on n’a pas besoin de forme spécifique :
class PaveDroitLong extends Pave {
PaveDroitLong(int n) { // constructeur
super(new FormeSimple(0,3, 9*n,3, 9*n,6, 0,6));
taille=n;
}
}Pavés signaux
On a besoin aussi de pavés signaux, par exemple pour les jonctions d’IPCS de l’article précédent :
On a besoin de trois formes, une forme combinée pour le mat et la cible, une forme pour le feu et une forme pour la voie. Pour la voie on a déjà la forme droite, pour le mat et la cible une forme polygonale convient bien, pour le feu c’est plus délicat. On pourrait utiliser les "ronds" de Processing (en fait des ellipses), mais ils ne suivront pas les transformations appliquées au pavé. Il faut donc construire un rond avec des PShape, quatre arcs de cercle obtenus avec des courbes de Bézier quadratiques (un seul point de contrôle) donnent un rond pas très rond, mais comme il est petit cela ne se voit pas. La forme feu :
class FormeFeu extends Forme { // feu pour les signaux
FormeFeu() { //constructeur
s.beginShape(); // quatre arcs de 90°
s.vertex(7.5,-0.5);
s.quadraticVertex(8.5,-0.5, 8.5,0.5);
s.quadraticVertex(8.5,1.5, 7.5,1.5);
s.quadraticVertex(6.4,1.5, 6.5,0.5);
s.quadraticVertex(6.5,-0.5, 7.5,-0.5);
s.endShape();
}
}Passons au pavé :
class PaveSignal extends Pave {
int feu; // couleur du feu pour le tco
PaveSignal(int f) { // constructeur
super(new Forme(3.4,3, 3.4,0.4, 6,0.4, 6,-1, 9,-1, 9,2, 6,2, 6,0.6, 3.6,0.6, 3.6,3),
new FormeFeu(),
new FormeDroit());
feu=f;
}
void dessiner() {
formes[0].dessiner(GRIS_FONCE); // cible et mat
formes[1].dessiner(feu); // feu
formes[2].dessiner(couleur); //voie
}
Pave manoeuvrer(boolean b) { // pour manoeuvres par clic
switch (feu) {
case ROUGE: feu=VERT; break;
case VERT: feu=ROUGE; break;
case VIOLET: feu=BLANC; break;
case BLANC: feu=VIOLET ; break;
}
return this;
}
}Le paramètre du constructeur est la couleur du feu que l’on veut voir affichée sur le TCO (rouge, violet, jaune, vert …). Cette couleur est mémorisée dans la variable feu.
La méthode dessiner() doit être redéfinie pour prendre en compte la couleur du feu, les trois formes sont dessinées successivement.
La méthode manoeuvrer() permet de changer la couleur du feu en simulant des ouvertures/fermetures simplifiées avec le même mécanisme que pour les aiguilles (clic de souris sur le pavé).
Retraits
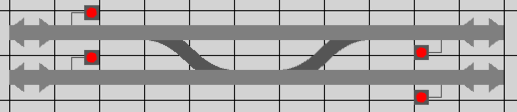
Sur un TCO il faut aussi matérialiser les zones, comme sur les TCOs de la SNCF une petite séparation est faite entre les pavés des zones. Voici ce que cela donne dans nos TCOs :
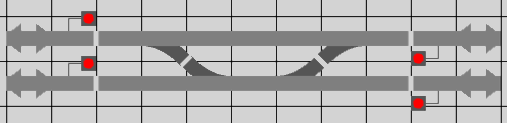
Cette séparation que nous appellerons "retrait" va être dessinée sur les pavés sous forme d’un petit rectangle de la couleur du fond, en pratique ce rectangle sera formé de deux demi-rectangles (un sur chacun des deux pavés adjacents) pour éviter d’éventuels défauts d’affichage dus à l’ordre d’affichage des pavés.
Pour un pavé il peut y avoir huit retraits possibles, quatre pour les parties droites et quatre pour les angles. Ces huit retraits serons nommés comme sur une rose des vents : nord, sud, est, ouest, nord-est, nord-ouest, sud-est et sud-ouest.
Les petits rectangles à dessiner sont en fait des formes particulières, on a besoin de deux formes, on choisit arbitrairement celles à l’est et au nord-est, on obtiendra les six autres avec des transformations.
Pour regrouper les deux formes retrait on commence par une classe abstraite Retrait, qui hérite de la classe Forme :
abstract class Retrait extends Forme {
final float Rd=0.5,Ra=Rd/1.75; // les tailles des retraits (droit et angle)
}On peut alors écrire les deux formes retrait dont on a besoin :
class RetraitDroit extends Retrait { // retrait est
RetraitDroit() { // constructeur
vertex(9,3, 9,6, 9-Rd,6, 9-Rd,3);
}
RetraitDroit(int n) { // constructeur
vertex(9*n,3, 9*n,6, 9*n-Rd,6, 9*n-Rd,3);
}
}
class RetraitAngle extends Retrait { // retrait nord est
RetraitAngle() { // constructeur
vertex(8,-1, 10,1, 10-Ra,1+Ra, 8-Ra,-1+Ra);
}
}La forme RetraitDroit a un deuxième constructeur destiné aux formes extensibles (droit et arc90).
Les retraits sont faits sur des pavés, il faut donc modifier cette classe pour les prendre en compte, il faut une structure de données pour mémoriser les retraits et des méthodes pour préciser le retrait, il faut aussi modifier la méthode dessiner() pour dessiner les retraits.
- Mémorisation des retraits
On ne connait pas à priori le nombre de retraits d’un pavé, Il faut donc utiliser une structure de donnée extensible, ArrayList convient bien. C’est une sorte de tableau dont la taille augmente automatiquement en fonction des besoins. En contrepartie il faut faire l’indiçage avec des méthodes ( add() et get()).
La classe ArrayList est ce que l’on appelle une classe générique, c’est à dire une classe paramétrée par un type. Ici on va l’utiliser pour mémoriser des formes. Voici la déclaration et l’instanciation :
ArrayList<Forme> retraits=new ArrayList<Forme>(); // les retraits
Les types pour la généricité sont écris entre les caractères ’<’ et ’>’ . Ici on a donc un tableau extensible dans lequel on peut mettre des Formes.
- Méthodes
Pour préciser les retraits on ajoute à la classe Pave, les huit méthodes nécessaires :
Class Pave {
...
ArrayList<Forme> retraits=new ArrayList<Forme>(); // les retraits
…
Pave retraitEst() { retraits.add(new RetraitDroit()); return this; }
Pave retraitSud() { retraits.add(new RetraitDroit().rotation()); return this; }
Pave retraitOuest() { retraits.add(new RetraitDroit().rotation(2)); return this; }
Pave retraitNord() { retraits.add(new RetraitDroit().rotation(3)); return this; }
Pave retraitNordEst() { retraits.add(new RetraitAngle()); return this; }
Pave retraitSudEst() { retraits.add(new RetraitAngle().rotation()); return this; }
Pave retraitSudOuest() { retraits.add(new RetraitAngle().rotation(2)); return this; }
Pave retraitNordOuest() { retraits.add(new RetraitAngle().rotation(3)); return this; }
Pave retraitEst(int n) { retraits.add(new RetraitDroit(n)); return this; }
Pave retraitSud(int n) { retraits.add(new RetraitDroit(n).rotation()); return this; }
Pave retraitOuest(int n) { retraits.add(new RetraitDroit(n).rotation(2)); return this; }
Pave retraitNord(int n) { retraits.add(new RetraitDroit(n).rotation(3)); return this; }
…
}Il y a quatre méthodes en plus pour les pavés extensibles. Comme précédemment ces méthodes ont un résultat artificiel pour pouvoir les enchaîner.
- Dessin
Il ne reste plus qu’a ajouter à la méthode dessiner() le dessin des retraits, cela doit se faire à la fin de la méthode (pour "cacher" les bouts des pavés avec le dessin des retraits) :
for (Forme f : retraits) f.dessiner(GRIS_FOND); // dessin des retraits
C’est ici encore un "forall" (pour toutes les Formes f de retraits ...), les retraits sont dessinés avec la couleur du fond.
Placement des paves
Dans la classe TCO il est pratique d’avoir des méthodes qui facilitent le placement des pavés. Le choix ici est fait de remplir le TCO comme on saisit un fichier texte, ligne par ligne et de gauche à droite. Quatre méthodes sont utilisées :
- une méthode pour ajouter un pavé
- deux méthodes pour espacer un ou plusieurs pavés
- une méthode pour passer à la ligne
On a besoin de deux variables pour gérer la ligne et la colonne courante :
int c=0,l=0; // pour la construction
void alaligne() { l++; c=0; assert l<LIGNES; } // aller a la ligne
void espacer() { c++; assert c<COLONNES; } // espacement
void espacer(int n) { c=c+n; assert c<COLONNES; } // espacement multiple
void ajouter(Pave p) { // ajout d'un pave
paves[c][l]=p;
c+=p.taille; assert c<COLONNES; // avancement fonction de la taille du pave
}Des tests sont faits pour ne pas déborder du TCO ("assert"). D’autres choix de méthodes de placement sont possibles.
Améliorations
Quais
Les quais sont des rectangles dont on peut choisir la largeur et éventuellement la couleur. Une classe PaveQuai est ajoutée avec deux constructeurs un avec juste la largeur du quai et l’autre avec la largeur et la couleur. La méthode dessiner() est redéfinie pour prendre en compte la couleur désirée.
Textes
Des textes sont bien pratiques pour nommer les voies, les provenances et destinations, ... Un PaveTexte est ajouté, ce pavé a une grande variété de constructeurs pour pouvoir, en plus du texte, choisir la taille, la couleur et le positionnement. Huit constructeurs sont prévus :
- un constructeur avec juste le texte
- un constructeur avec le texte et une taille (réel)
- un constructeur avec le texte et une couleur (entier)
- un constructeur avec le texte, une taille et une couleur
- quatre constructeurs comme les précédents mais avec deux paramètres (réels) en plus permettant d’affiner la position du texte (en hauteur et en largeur)
La méthode dessiner() est redéfinie pour prendre en compte les paramètres. Par défaut le texte est centré au milieu du pavé, mais les deux paramètres optionnels de positionnement permettent de le placer où on veut, ils précisent un décalage en x et un décalage en y (positifs ou négatifs).
Un exemple de textes combinés avec des quais :
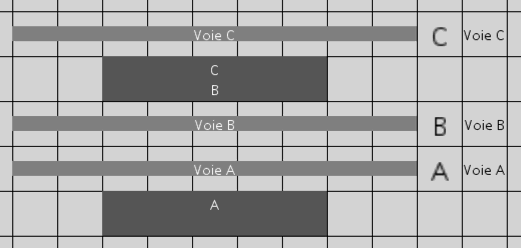
Signaux
On ne peut pas encore faire grand chose avec les signaux, mais on peut toutefois faire apparaître une icône du signal réel quand la souris passe sur un pavé signal. Voici quelques exemples de ces icônes :

|
Toujours avec le TCO d’IPCS cela donne :
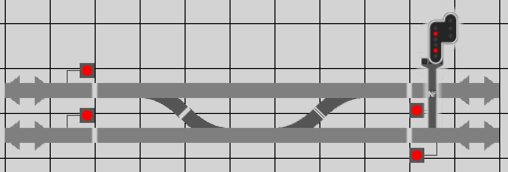
Il faut bien sûr préciser le signal (ces signaux seront aussi utilisés par la suite), pour cela on rajoute à la classe PaveSignal un nouveau constructeur de type "signal" et on retouche la méthode manoeuvrer() :
class PaveSignal extends Pave {
Signal signal=null; // le signal
int feu; // couleur du feu pour le tco
PaveSignal(int f) { // constructeur
super(new FormeSimple(3.4,3, 3.4,0.4, 6,0.4, 6,-1, 9,-1, 9,2, 6,2, 6,0.6, 3.6,0.6, 3.6,3),
new FormeFeu(),
new FormeDroit());
feu=f;
}
PaveSignal(Signal s) { // constructeur
super(new FormeSimple(3.4,3, 3.4,0.4, 6,0.4, 6,-1, 9,-1, 9,2, 6,2, 6,0.6, 3.6,0.6, 3.6,3),
new FormeFeu(),
new FormeDroit());
signal=s; feu=s.feu.couleur;
}
void dessiner() {
formes[0].dessiner(GRIS_FONCE); // cible et mat
formes[1].dessiner(feu); // feu
formes[2].dessiner(couleur); //voie
for (Forme f : retraits) f.dessiner(GRIS_FOND); // dessin des retraits
}
Pave manoeuvrer(boolean b) { // pour manoeuvres par clic
if (signal!=null) {
if (signal.ferme()) { if (b) signal.ouvrirManoeuvre(); else signal.ouvrir(); } else signal.fermer();
couleur=signal.feu.couleur;
} else {
switch (feu) {
case ROUGE: feu=VERT; break; // avertissements ??? (vl)
case VERT: feu=ROUGE; break;
case VIOLET: feu=BLANC; break;
case BLANC: feu=VIOLET ; break;
}
}
return this;
}
...
}Le deuxième constructeur mémorise le signal, et extrait de ce signal la couleur à mettre sur le TCO. La méthode manoeuvrer() est modifiée pour prendre en compte le signal et pour pouvoir le manœuvrer, un clic gauche l’ouvre en mode "ligne", un clic droit en mode "manoeuvre".
Pour les signaux on va reprendre ceux de l’article Un gestionnaire en C++ pour votre réseau (2). Dans cet article les classes pour les signaux sont écrites en C++, on va ici les traduire en Java, voir l’article Processing pour nos trains pour les passages d’un langage à l’autre. Mais toutes les explications sur l’écriture des classes restent les mêmes.
Comme nous n’avons pas encore les moyens d’accéder aux signaux précédents et suivants (mais cela viendra !), on va se contenter ici d"une version "édulcorée" des signaux.
Pour l’instant on ne peut pas faire grand chose avec les signaux (mais cela viendra), mais on peut tout de même, comme on en a parlé précédemment, dessiner le signal réel quand la souris passe sur le pavé signal.
Dans l’article précédent il y avait déjà un gestionnaire d’événements pour les clics de souris :
void mouseClicked() { int l,c; ; Pave p;
l=(mouseY-BORDURE)/TAILLE_CASE/(int)ZOOM; // calcul de la ligne
c=(mouseX-BORDURE)/TAILLE_CASE/(int)ZOOM; // calcul de la colonne
if (l<0 || l>=LIGNES || c<0 || c>=COLONNES) return; // pas dans tco
p=tco.paves[c][l]; // obtension du pave
if (p!=null) p.manoeuvrer(mouseButton==RIGHT); // manoeuvre des aiguilles
}Sur le même modèle on écrit un gestionnaire des mouvement de la souris :
PaveSignal paveSignalSelectionne=null;
void mouseMoved() { int l,c; ; Pave p;
l=(mouseY-BORDURE)/TAILLE_CASE/(int)ZOOM; // calcul de la ligne
c=(mouseX-BORDURE)/TAILLE_CASE/(int)ZOOM; // calcul de la colonne
if (l<0 || l>=LIGNES || c<0 || c>=COLONNES) return; // pas dans tco
p=tco.paves[c][l]; // obtension du pave
if (p==null || !(p instanceof PaveSignal)) { paveSignalSelectionne=null; return; }
paveSignalSelectionne=(PaveSignal)p;
}La variable globale paveSignalSelectionne mémorise le pavé sélectionné (sinon null). L’opérateur instanceof permet de tester la classe réelle d’un objet, ici un PaveSignal
Reste à dessiner le signal quand il faut, cela se fait dans le TCO tout à la fin de la méthode dessiner() pour que le signal soit dessiné au dessus de tout.
void dessiner() {
…
if (paveSignalSelectionne!=null) { // dessin de la cible du signal
for (l=0; l<LIGNES; l++) for (c=0; c<COLONNES; c++) { // dessin des paves
p=paves[c][l]; // un des paves
if (p!=null && p==paveSignalSelectionne) {
translate(c*TAILLE_CASE,l*TAILLE_CASE);
dessinSignal();
}
}
}
} La méthode dessinSignal() est assez compliquée, on ne fera ici que décrire son fonctionnement, pour plus d’information voir les fichiers accompagnant l’article, cette méthode comporte plusieurs étapes :
- réglage du zoom
- obtention du signal
- obtention de l’image du signal en utilisant la méthode
icone()de la classe signal - recherche du centre du mat du signal pour le positionner au centre du pavé
- dessin de l’image
La méthode icone() charge la bonne image, un mécanisme de cache est mis en oeuvre pour accélérer les chargements. La méthode permet aussi d’avoir un "halo" autour de l’image, pour qu’elle ressorte bien au dessus des composants du TCO, quand son paramètre est "vrai".
Le halo est fait de la manière suivante, un pixel de la couleur du fond est ajouté tout autour de l’image en suivant son contour, cette opération est répétée seize fois avec un pixel de plus en plus transparent. Plusieurs méthodes utilitaires sont nécessaires.
Fichiers
Quelques précisions sur les fichiers accompagnant l’article :
Le dossier "Exemple_2_0" contient le programme Processing conforme aux descriptions de l’article.
Améliorations
Le dossier "Exemple_2_1" contient une version améliorée du précédent. Cette "amélioration" se fait essentiellement avec la prise en compte des signaux réels. Deux dossiers contiennent une grande variété d’icônes de signaux lumineux et de signaux mécaniques.
Aide
Comme pour l’article précédent, une petite application "Aide2" facilite l’écriture des TCOs, notamment pour les signaux.
Cette application propose trois palettes flottantes :
- une palette avec les pavés de base enrichis des butoirs et des sens
- une palette avec les pavés extensibles droit et arc90, ajustables avec la molette de la souris
- une palette avec les signaux, trois choix de signaux sont sélectionnables avec les trois boutons ("lum", "bal" et "mec") signaux lumineux, signaux de BAL et signaux mécaniques.
Avec cette application Processing est poussé dans ses derniers retranchements, et "bogue" de temps en temps dans la gestion de mémoire, relancer dans ce cas.
Le mode d’emploi est le même que celui de l’aide du précédent article. Pour changer la taille des pavés extensibles utiliser la molette de la souris.
Bilan
On a maintenant à peu près tout ce qu’il faut pour dessiner des TCOs, on peut rajouter assez facilement des éléments manquants, par exemple des demi pavés :

L’utilisation principale des demi-pavés est de pouvoir faire des séparations de zones (retraits) au milieu d’un pavé droit ou biais. En pratique cela implique généralement de mettre deux demi-pavés dans une même case du TCO, il faut alors une structure de données adaptée pour mémoriser les pavés.
Exemple des jonctions croisées :

|

|
Ces jonctions posent un problème pour le cœur du croisement car les pavés se chevauchent, pour que cela soit joli il faut sur-dessiner le cœur de croisement en fonction de la position des aiguilles (noter que les quatre appareils de voie encadrant le croisement peuvent êtres quelconques : aiguilles simples, aiguilles doubles voire croisements).
Autre exemple une plaque tournante :

Bien évidemment elle peut être animée.
Concernant la géométrie des pavés (largeur, hauteur, épaisseur de la voie, …), il est facile d’en changer, voici quelques exemples :
La largeur est deux fois celle de la hauteur, les pavés font 18x9 points.
Là on joue sur l’épaisseur de la voie, les pavés font 10x10 points.
Sur les pavés de base (ceux de l’article précédent) il n’y a que cinq modifications à faire, revoir les contours des pavés de base (droit, biais et Arc45) et revoir les transformations des formes (symétrie et rotation), c’est pratiquement tout. Sur les autres pavés cela demande un peu plus de travail.
Il y a quelques précautions à prendre, il faut que les bouts des pavés se raccordent parfaitement aux autres, il importe aussi que l’épaisseur des biais soit le plus possible égale celle des droits.
Dans l’article précédent on a fait des choix pour la géométrie des pavés avec une taille de pavés 9x9 points, ces choix sont motivés par deux choses, premièrement avoir des droits et des biais d’épaisseur presque identique (ici 3 et 2.828), deuxièmement avoir des voies suffisamment épaisses pour pouvoir écrire des informations dedans, par exemple des noms de trains, mais aussi pour avoir assez d’épaisseur pour pouvoir faire circuler des trains virtuels, on en parlera par la suite.
On pourrait paramétrer les programmes pour prendre en compte les variantes dans la géométrie des pavés, mais cela rendrait le programme totalement illisible au niveau des formes.
Dans de prochains articles on va faire des traitements sur l’ensemble des pavés pour fabriquer automatiquement tout ce qui est nécéssaire au fonctionnement des zones. On s’intéressera aussi à l’interface entre le TCO et un gestionnaire de réseau sur Arduino.