On a vu au début de « Types, constantes et variables » que l’Arduino, comme tous les ordinateurs, calcule en binaire. Les nombres qu’il manipule sont codés sur 8 (1 octet), 16 (2 octets) ou 32 (4 octets) bits. Bit signifie BInary digiT, donc littéralement chiffre binaire. Ainsi, pour des nombres non signés, c’est à dire exclusivement positifs, la valeur 0 en décimale sera codée 00000000 sur 8 bits, la valeur 1 sera codée 00000001, la valeur 2 sera codée 00000010. etc. La valeur maximum sur 8 bits, 255, sera codée 11111111. Vous pouvez vous référer à « Systèmes de numération » pour en savoir plus à ce sujet.
Calculer avec l’Arduino
Calculer avec l’Arduino (2)
Les opérations sur les bits
.
Par :
DIFFICULTÉ :★★☆
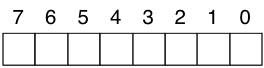
Dans ce qui suit, les bits sont numérotés comme montré dans la figure ci-dessous. Chaque case peut contenir un bit, au dessus on a le numéro du bit. Le bit 0 est le bit le plus à droite, le bit 7 est le bit le plus à gauche. Ceci est donc un octet.
Opérateurs sur les bits
Plusieurs opérateurs permettent de manipuler les bits. Ces opérateurs calculent sur tous les bits de même rang de leur opérandes, on dit que ce sont des opérateurs bit à bit. Dans cette catégorie, nous trouvons les classiques et, ou, ou exclusif et non.
D’autres opérateurs permettent d’effectuer des décalages.
Pour tous ces opérateurs, la variante combinée avec une affectation existe. Voir « Calculer avec l’Arduino (1) ».
Le & (et bit à bit)
l’opérateur & effectue un et bit à bit. Pour chacun des bits de même rang des opérandes et du résultat, le bit résultat est à 1 si les 2 bits opérandes sont à 1. Le bit résultat est à 0 sinon. Le programme ci-dessous montre ce qui se passe pour un et de deux variables :
byte a = 85; // 85 en base 10 est égal à 01010101 en binaire
byte b = 15; // 15 en base 10 est égal à 00001111 en binaire
byte c = a & b; // Le résultat est égal à 00000101 en binaire
Serial.print("c (dec) = ");
Serial.print(c);
Serial.print(", c (bin) = ");
Serial.println(c,BIN);}L’affichage sera
c (dec) = 5, c (bin) = 101
Le | (ou bit à bit)
l’opérateur | effectue un ou bit à bit. Pour chacun des bits de même rang des opérandes et du résultat, le bit résultat est à 1 si l’un, au moins, des 2 bits opérandes est à 1. Le bit résultat est à 0 si les deux bits opérandes sont à 0. Le programme ci-dessous montre ce qui se passe pour un ou de deux variables :
byte a = 85; // 85 en base 10 est égal à 01010101 en binaire
byte b = 15; // 15 en base 10 est égal à 00001111 en binaire
byte c = a | b; // Le résultat est égal à 01011111 en binaireLe ^ (ou exclusif bit à bit)
l’opérateur ^ effectue un ou exclusif bit à bit. C’est le ou de « fromage ou dessert ». Pour chacun des bits de même rang des opérandes et du résultat, le bit résultat est à 1 si exactement un des 2 bits opérandes est à 1. Autrement dit, le résultat est à 1 si les deux bits sont différents et à 0 si ils sont identiques. Le programme ci-dessous montre ce qui se passe pour un ou exclusif de deux variables :
byte a = 85; // 85 en base 10 est égal à 01010101 en binaire
byte b = 15; // 15 en base 10 est égal à 00001111 en binaire
byte c = a ^ b; // Le résultat est égal à 01011010 en binaireLe ~ (non bit à bit)
l’opérateur ~ effectue un non bit à bit. Chaque bit de l’opérande est inversé : le non de 0 est 1 et le non de 1 est 0. Le programme ci-dessous montre ce qui se passe pour un non appliqué à la variable a :
byte a = 85; // 85 en base 10 est égal à 01010101 en binaire
byte b = ~a; // Le résultat est égal à 10101010 en binaireOpérateurs de décalage
Les opérateurs de décalage permettent de décaler les bits à gauche ou à droite d’un certain nombre de bits.
L’opérateur << (décalage à gauche)
L’opérateur de décalage à gauche décale le premier opérande vers la gauche d’un nombre de bits égal au second opérande. Les bits laissées libres à droite par le décalage sont remplis de 0. Ainsi, dans le programme suivant :
byte a = 5; // 5 en base 10 est égal à 00000101 en binaire
byte b = a << 2; // Le résultat est égal à 00010100 en binaire5 est décalé à gauche de 2 bits. Ceci revient à multiplier par 22, soit 4 [1]. Le résultat est donc 20 ce qui correspond bien à 00010100 en binaire. Les bits décalés au delà des bits disponibles sont perdus.
Il peut se produire un débordement lors d’un décalage de la même manière qu’un débordement peut se produire lors d’un autre calcul. Un débordement n’est pas forcément dommageable car une donnée peut ne pas être un nombre mais seulement un ensemble de bits qui représentent, individuellement ou par groupes, une ou plusieurs informations.
Le débordement, si il existe, dépend du type de la donnée que l’on décale. Si il s’agit d’une donnée non signée comme l’est byte, et si des bits à 1 sont décalés au delà du bit le plus à gauche, et donc perdus, on a un débordement. Ainsi, les lignes suivantes produisent un débordement :
byte a = 5; // 5 en base 10 est égal à 00000101 en binaire
byte b = a << 6; // Le résultat est égal à 01000000 en binaireLe décalage est équivalent à la multiplication de 5 par 26. Or, le résultat de cette multiplication devrait être 320 (26 est égal à 64 et 5 multiplié par 64 donne 320). 320 ne pouvant pas être codé sur un octet, on a donc un débordement.
Dans le cas d’une donnée signée comme par exemple int8_t qui n’a pas d’équivalent Arduinisé, c’est un peu plus compliqué et il faut se pencher sur le codage des nombres signés pour comprendre.
Un petit mot sur le codage des nombres signés
Nous avons vu que les nombres étaient codés en binaire dans « Types, constantes et variables ». Les nombres signés sont codés en complément à 2. Le bit de poids fort, c’est à dire le bit le plus à gauche est le bit de signe. Un nombre positif a son bit de signe à 0, un nombre négatif a son bit de signe à 1. Il ne suffit pas de changer le bit de signe pour changer le signe d’un nombre, c’est un peu plus compliqué. Prendre l’opposé d’un nombre consiste à inverser tous les bits et à ajouter 1 au nombre obtenu. Par exemple le nombre 1 est codé 00000001. Pour calculer son opposé, c’est à dire –1, les bits sont inversés, ce qui donne 11111110. Puis on ajoute 1 ce qui donne 11111111. –1 est donc codé 11111111. -2 est codé 11111110, -3 est codé 11111101 et ainsi de suite jusqu’à -128, le plus petit nombre signé représentable sur un octet qui est codé 10000000.
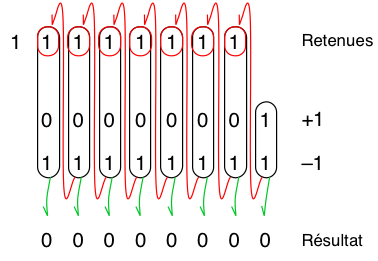
Ce codage qui peut sembler bizarre a en fait pour but de permettre les opérations arithmétiques sans avoir à se préoccuper du fait que les nombres soient signés ou non. Par conséquent l’Arduino ne fait pas la distinction sauf en de très rares cas dont nous allons voir un exemple un peu plus loin. Par exemple, ajouter 1 et –1 se fait tout naturellement par une addition binaire comme montré à la figure ci-dessous.
L’addition en binaire se réalise comme l’addition en base dix, à la différence qu’un résultat plus grand que 1 donne lieu à une retenue (les flèches rouges dans la figure ci-dessus). Sur un bit, 0 + 0 donnera bien entendu 0 ; 0 + 1 donnera 1 ; 1 + 1 donnera 10, c’est à dire 0 et je retiens 1 et 1 + 1 + 1, il peut y avoir une retenue à ajouter, donnera 11 c’est à dire 1 et je retiens 1.
La retenue sortante tout à gauche étant perdue, le résultat est bien égal à 0.
Ici, un débordement peut donc se produire si un bit décalé à gauche vient changer la valeur du bit de signe et donc changer le signe du nombre. Prenons comme exemple 127 en base dix qui se code 01111111 en binaire signé. En le décalant à gauche de 1 bit, on obtient 11111110. c’est à dire -2. Prenons -64 en base dix qui se code 11000000 en binaire signé. Un décalage à gauche de 2 bits donnera 00000000, c’est à dire 0. Dans les deux cas on a un débordement.
L’opérateur >> (décalage à droite)
L’opérateur de décalage à droite décale le premier opérande vers la droite d’un nombre de bits égal au second opérande. Dans le programme suivant un décalage de 4 bits à droite est effectué :
byte a = 176; // 176 en base 10 est égal à 10110000 en binaire
byte b = a >> 4; // Le résultat est égal à 00001011 en binaire, soit 11Ici 176 est décalé à droite de 4 bits, ce qui revient à effectuer une division entière par 24 = 16. 176 ÷ 16 est bien égal à 11.
Le traitement est différent selon que la donnée est signé ou non signée. Pour une donnée non signée, les bits de gauche laissés libres par le décalage sont remplis de 0 comme dans l’exemple ci-dessus. Pour une donnée signée, les bits de gauche laissés libres par le décalage sont remplis avec le bit de signe. Ainsi +2, 00000010 en binaire signé, décalé à droite de 1 bit donne 00000001 c’est à dire 1. –2, 11111110 en binaire signé, décalé à droite de 1 bit donne 11111111, c’est à dire –1.
Modifier les bits individuellement
En combinant ces opérateurs, on peut modifier les bits individuellement. Supposons par exemple que l’on veuille mettre à 1 le bit le plus à gauche d’une variable a de type byte sans toucher aux autres bits. On écrira :
byte a = 111; // 111 en base 10 est égal à 01101111 en binaire
a |= 1 << 7; // Le résultat est égal à 111011111 << 7 donne 10000000 et |= effectue un ou binaire entre a et 10000000, ce qui a pour effet de forcer à 1 le bit le plus à gauche.
Pour mettre un bit à 0, on écrira :
byte a = 255; // 255 en base 10 est égal à 11111111 en binaire
a &= ~(1 << 7); // Le résultat est égal à 01111111Comme précédemment, 1 << 7 donne 10000000, l’opérateur ~ inverse tous les bits pour donner 01111111 et &= effectue un et binaire entre a et 01111111, ce qui a pour effet de forcer à 0 le bit le plus à gauche.
Pour inverser un bit, on écrira :
byte a = 255; // 255 en base 10 est égal à 11111111 en binaire
a ^= 1 << 7; // Le résultat est égal à 01111111^= effectue un ou exclusif binaire entre a et 10000000, ce qui a pour effet de d’inverser le bit le plus à gauche. En effet, si ce bit est 0, le ou exclusif avec 1 donne 1 et si ce bit est 1, le ou exclusif avec 1 donne 0. Les autres bits ne sont pas touchés car le ou exclusif d’un bit avec 0 donne la valeur du bit.
Modifier plusieurs bits simultanément
Pour tous les opérateurs présentés, il est bien entendu possible de modifier plusieurs bits simultanément. Par exemple, l’inversion des bits 0, 2 et 4 s’écrira de la manière suivante :
byte a = 255; // 255 en base 10 est égal à 11111111 en binaire
a ^= 1 << 0 | 1 << 2 | 1 << 4; // Le résultat est égal à 11101010Il suffit donc de faire un ou bit à bit : | de 1 décalé à gauche du numéro du bit pour chacun des bits que l’on veut à 1 dans l’opérande. Les autres bits sont implicitement à 0.
C’est compliqué tout ça, il n’y a pas plus simple ?
La bibliothèque de base de l’Arduino fournit plusieurs fonctions qui facilitent la manipulation de bits. Ces fonctions permettent sans aucun doute une plus grande lisibilité du code. Elles sont aussi efficaces que l’usage direct des opérateurs sauf dans le cas où il s’agit de manipuler plusieurs bits simultanément. En effet, il faut utiliser plusieurs fois la fonction, une fois pour chaque bit.
bitRead
bitRead(x, n) permet de lire un bit. Le premier argument, x est la donnée d’où on lit le bit, le second argument, n est le numéro du bit. Par exemple :
byte a = 5; // 5 en base 10 est égal à 00000101 en binaire
byte b = bitRead(a,2);mettra dans b le bit 2 de a, c’est à dire le 2e 1 en partant de la droite.
bitWrite
bitWrite(x, n, b) permet d’écrire un bit. Le premier argument, x est la donnée où on écrit le bit, le second argument, n est le numéro du bit et le 3e, b est la valeur à écrire, 0 ou 1.
byte a = 5; // 5 en base 10 est égal à 00000101 en binaire
bitWrite(a,3,1);écrira un 1 dans le bit 3. La valeur contenue dans a sera donc 00001101.
bitSet
bitSet(x, n) permet de mettre à 1 un bit. Le premier argument, x est la donnée où on écrit le bit, le second argument, n est le numéro du bit. Cette fonction est l’équivalent d’une bitWrite(x,n,1).
bitClear
bitClear(x, n) permet de mettre à 0 un bit. Le premier argument, x est la donnée où on écrit le bit, le second argument, n est le numéro du bit. Cette fonction est l’équivalent d’une bitWrite(x,n,0).
En résumé
La table ci dessous présente l’usage de chacun des opérateurs et, le cas échéant, de leur équivalent Arduino pour effectuer la mise à 1, la mise à 0, la mise à une valeur quelconque et l’inversion de bit.
| Tâche à accomplir | Fonction Arduino | Opérateur C |
|---|---|---|
| Mise à 0 du bit n de x | bitClear(x, n); |
x &= ~(1 << n); |
| Mise à 1 du bit n de x | bitSet(x, n); |
x |= 1 << n; |
| Mise à b du bit n de x | bitWrite(x, n, b); |
— [2] |
| Inversion du bit n de x | — | x ^= 1 << n; |
Mais à quoi tout cela peut-il servir ?
Accéder aux bits individuellement a de multiples usages. C’est par exemple nécessaire si on veut accéder à certains bits des registres de contrôle des périphériques comme le GPIO, l’I2C ou le SPI. Mais c’est également nécessaire pour gagner de la place en mémoire. Imaginons par exemple que nous souhaitions gérer un grand nombre de capteurs tout ou rien disséminés sur plusieurs Arduino en réseau (CAN par exemple) et que l’un des Arduino centralise l’état de ces capteurs dans un tableau dont les valeurs sont rafraîchies périodiquement via le réseau. L’état de chaque capteur est un booléen, vrai ou faux, c’est à dire en fait 1 ou 0. Si nous construisons un tableau de booléens, chaque capteur occupera un octet. Or un seul bit suffit et allouer un bit à chaque capteur permet d’occuper 8 fois moins de mémoire.
Si on représente le numéro d’un capteur sur 16 bits, on peut décomposer ce numéro en deux parties : les 13 bits de poids fort sont l’index dans le tableau d’octets et les 3 bits de poids faible le numéro de bit dans l’octet. 3 bits car sur 3 bits on code exactement 23 = 8 valeurs, de 0 à 7, ce qui correspond au nombre de bits dans un octet. Extraire l’index consiste donc à décaler le numéro de capteur de 3 bits à droite. Extraire le numéro de bit dans l’octet revient à ne garder que les 3 bits de poids faible en faisant un & avec 0b0000000000000111 [3]. Si nous voulons connaître l’état d’un capteur dans le tableau, nous pouvons écrire la fonction suivante.
bool lireCapteur(const uint16_t numero)
{
const uint16_t index = numero >> 3;
const uint8_t numeroDeBit = numero & 0b0000000000000111;
return (tableCapteurs[index] & (1 << numeroDeBit) != 0;
}Mettre à jour un capteur dans le tableau consiste à écrire un bit au bon endroit. Pour cela nous allons utiliser le | mais avant de mettre la nouvelle valeur il faut mettre ce bit à 0 et donc faire un & avec un octet composé de 1 sauf là où nous voulons mettre le bit à 0, ce qui s’obtient par l’expression ~(1 << numeroDeBit). La fonction suivante fait le travail.
void ecrireCapteur(const uint16_t numero, const bool valeur)
{
const uint16_t index = numero >> 3;
const uint8_t numeroDeBit = numero & 0b0000000000000111;
uint8_t octet = tableCapteurs[index];
octet &= ~(1 << numeroDeBit);
octet |= (valeur != 0) << numeroDeBit;
tableCapteurs[index] = octet;
}C’est avec cet exemple, que j’espère parlant, que nous concluons cet article.
[1] Dans toutes les bases b, un décalage de n chiffres à gauche correspond à une multiplication par bn. Un décalage de n chiffres à droite correspond à une division entière par bn. Par exemple, en base 10, décaler 1 à gauche de 3 chiffres donne 1000 = 103.
[2] Ceci nécessite une opération conditionnelle que nous verrons ultérieurement.
[3] Il est possible de donner des constantes en binaire en préfixant le nombre, qui ne doit bien évidemment ne contenir que des 0 et des 1, par 0b ou 0B.